Another winner of the CoS Science Communication Writing Competition Merit Prize, Mehedi Hasan from the School of Physical and Mathematical Sciences!
Mehedi wrote about “Non-Abelian Artificial Gauge Field.” Congratulations, Mehedi!
Mehedi receiving his prize from the Dean of Science, Professor Simon Redfern
Non-Abelian Artificial Gauge Field
Written by Mehedi Hasan
A charged particle in a uniform magnetic field undergoes circular motion. The Lorentz force that keeps the particle in a circular orbit, reverses direction for the opposite charge. In the framework of classical electrodynamics, one can deterministically predict the trajectories of a classical particle, for a known electric and magnetic field configuration. However, there is an equivalent and succinct description of the same electromagnetic field via a single quantity named gauge field.
The mathematical description of the gauge field is inherently appealing, however, there is one little caveat – gauge field is not unique for a given electromagnetic field. Thus, despite the elegance in its representation, physicists did not take gauge field as something ‘physical’ other than a mathematical curiosity. However, our understanding changed radically after 1959 as Aharonov and Bohm theoretically pointed out the physical nature of gauge field, and this was experimentally verified in the following year. Nowadays, gauge field is the driving-horse for our understanding of a plethora of phenomena ranging from high-energy physics to lasers and waveguide. To theoreticians, gauge field is even more real than to us mortals. That’s why each time a theorist is faced with a problem where a particle is interacting with another field, gauge field is the sharpest knife in the drawer.
Depending on the fact whether the sequence of multiplication is important or not, during the multiplication of two components of a gauge field, gauge field is classified into two categories. Firstly, it can be Abelian where the multiplication of different components is insensitive of sequence – just like numbers: 2×3 = 3×2 . For example, the gauge field of a plane electromagnetic wave is an Abelian gauge field. And the second type of gauge field is the non-Abelian gauge field, where each component is a matrix. This kind of matrix-valued gauge field was introduced in physics by C-N. Yang, R. Mills, and R. Shaw, to understand how nucleons (protons and neutrons) hold together. Non-Abelian gauge field is much richer in phenomenology due to its matrix-valued nature.
With the wake of quantum simulation, an idea put forward by Richard Feynman, atomic physicists have devised schemes where, with neutral atoms and lasers, one can emulate the same kind of non-Abelian gauge field that are found inside nuclear matter. The advantage of having to realize the non-Abelian gauge field with lasers and atoms, is that one can study a vast class of interesting Hamiltonians, in a controlled environment at temperature of few tens of nanokelvin.
|
 Figure 1(a). Toy model for the generation of artificial gauge field with neutral atoms |
|
 Figure 1(b). A typical symmetric expansion of an atomic cloud in an Abelian gauge field |
|
 Figure 1(c). Asymmetrically expanding density of an atomic cloud inside a non-Abelian gauge field |
To get of a glimpse of how such a non-Abelian gauge field appears, consider the scheme in Fig. 1(a). The two counter-propagating lasers L1 and L2 (shown by blue and orange arrows, respectively) are applied to the atoms (schematically shown green and the image is not to scale). By exploiting the selection-rules of quantum mechanics, everything boils down to the following two rules:
- If an atom is in the state a, it can only absorb light from laser L1, to reach the excited state e. Afterwards, the atom can relax back to state b while it emits a photon co-propagating with L2.
- And the same happens for an atom in state b: it only absorbs light from L2 to reach the excited state e, and the atom subsequently can go back to state a by emitting a photon that co-propagates with laser L1.
This seemingly simple set of rules can give rise to a plethora of interesting phenomena. For example, if we watch closely, we see that the atoms in state a will be pushed to the right, after absorbing light from L1, and it will be again pushed to the right, when the atom relaxes from the excited state by emitting a photon co-propagating with L2, due to momentum conservation. This implies that an atom in state a, will always be pushed to the right. And by a similar argument, an atom in state b will always be pulled to the left. Therefore, the directions of force (left or right) are determined by the occupied atomic states (state a or state b) – similar to Lorentz force where the oppositely charged particles feel a different force in the same electromagnetic field.
In the above situation, the atomic states are playing the role of ‘charge’ for the Lorentz-like force. As one writes-down the governing equations for this phenomenon, matrix-valued gauge field pops out. This is the key reason for the emergence of non-Abelian gauge field. We parenthetically note that the gauge field here is solely induced externally by lasers that one can control at will. For this reason, we usually call it an artificial non-Abelian gauge field.
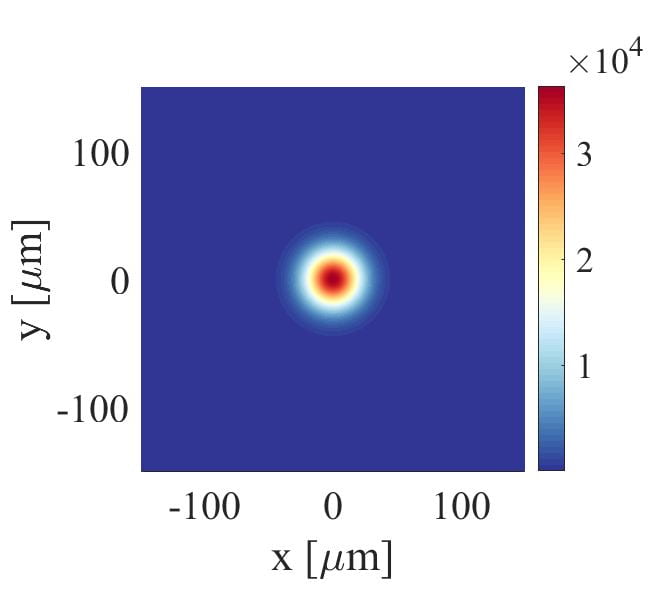
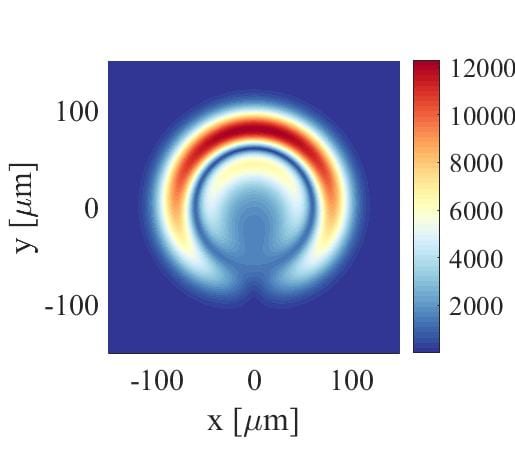
In the lab of Prof. David Wilkowski at SPMS of NTU, by playing with different configurations and polarizations of lasers, we create artificial non-Abelian gauge field for ultracold neutral atoms, at a temperature around 30 nK. In our lab, the non-Abelian nature of the gauge field was experimentally revealed by a set of experiments [1]. Currently, one of the key directions of the lab is to experimentally understand how an atomic cloud of symmetric-shape, evolves under the influence of non-Abelian gauge field. For example, a symmetric wavepacket stays symmetric if the gauge field is Abelian, as shown in Fig. 1(b). However, in a non-Abelian gauge field, the expansion of the density is manifestly asymmetric, as shown in Fig. 1(c). Things become much more intricate and exciting as one turns-on interaction between atoms, in the presence of non-Abelian gauge field. Understanding this kind of many-body system is challenging and rewarding. We are looking forward to the next few years regarding our experiments on the non-Abelian gauge field. Stay tuned!
References:
[1] F. Leroux et al. “Non-Abelian and adiabatic geometric transformation in a cold atomic gas”, Nature Communications 9, 3580 (2018).