The NTU research team that developed the theory of Quantum Reservoir Processing. From left: Dr Sanjib Ghosh, Huawen Xu, Nanyang Assistant Professor Timothy Liew, and Dr Tanjung Krisnanada. Photo credit: M. Fadly.
Go, a board game that emphasizes strategy, intuition, and pattern recognition, is a mainstay of Machine Learning (ML) research. One of the most famous ML breakthroughs occurred in 2016, when the AlphaGo program defeated Lee Sedol, the top-ranked human Go player at the time, winning four out of the five games played. AlphaGo’s performance hinged on its biologically inspired “neural network” computing architecture, which recognizes patterns efficiently by representing complicated data in a high-dimensional “feature space”.
The emerging research field of Quantum Machine Learning aims to combine quantum computing with neural networks to create computers with unprecedented capabilities. In a recent series of papers, we have designed a new type of quantum computer called a Quantum Reservoir Processor, which may be able to tackle certain notoriously difficult information processing problems in quantum physics.
Quantum computers have the potential to perform certain computationally demanding tasks, such as factoring large numbers, much faster than any possible classical computer. However, most of the quantum computers currently being developed are unrelated to neural networks. With the rise of ML as a computing paradigm, physicists and computer scientists are looking into whether the power of quantum computing can be brought to bear on ML problems such as pattern recognition.
To understand the importance of pattern recognition as a computing problem, think again about the game of Go. In principle, it is possible to design an algorithm that proposes moves by applying a set of conditions to the current game state. However, given the complexity of the game, it is impossible in practice to design a set of conditions comprehensive enough to handle the scenarios encountered in a typical match. To get around this problem, a classical neural network learns the most important features of the game state for itself, by training on millions upon millions of example games.
One possible connection between quantum computing and ML is that quantum computers, like neural networks, derive their effectiveness from representing data in a high-dimensional space. In a quantum computer, computing takes place in a gigantic “Hilbert space” representing the set of all possible states of a quantum system. Our concept of the Quantum Reservoir Processor is inspired by this fact.
A Device to Recognize Quantum Patterns
In a 2019 paper in npj Quantum Information, we showed how a class of neural network called a reservoir network can be used to formulate a new type of quantum processor, which can be trained to recognize patterns in quantum states [1].
Schematic of a Quantum Reservoir Processor. Figure excerpted from Ref. [1].
Unlike a typical neural network, the connections between the nodes in the Quantum Reservoir Processor are fixed rather than adjustable. This makes the Quantum Reservoir Processor easier to implement than a fully-fledged quantum computer. Conceptually, it can be regarded as a powerful quantum processor (the reservoir) connected to a trainable classical processor.
Asst. Prof. Timothy Liew explaining the concept of quantum reservoir processing. Photo credit: M. Fadly.
Disentangling a Quantum Enigma
To demonstrate the usefulness of the Quantum Reservoir Processor concept, we showed that it can be trained to identify whether a quantum state possesses a subtle feature known as “entanglement”.
Entanglement is a phenomenon that governs the relationship between the quantum states of two or more particles. If entanglement is present, measurements performed on one particle can subtly affect measurements on the other particle – a state of affairs once described by Albert Einstein as “spooky action at a distance”.
Identifying the presence and degree of quantum entanglement in an arbitrary quantum system is a difficult open problem. For a simple quantum system like a pair of qubits, there are well-established procedures for characterizing entanglement, but for technical reasons it is difficult to extend these procedures to quantum systems of higher complexity.
Using computer simulations, we investigated whether a Quantum Reservoir Processor can be trained to identify entanglement in a quantum state. It would have to learn to recognize the subtle features of the input state signifying quantum entanglement, without any prior knowledge of the standard procedures that human researchers had devised for quantifying entanglement.
We trained the Quantum Reservoir Processor with a set of 200 examples, called squeezed thermal states, whose levels of quantum entanglement are known beforehand. We then tested the system using a new type of entangled quantum state called a Bell state. Remarkably, even though the Quantum Reservoir Processor had never encountered Bell states during training, it could accurately characterize the entanglement of the Bell states!
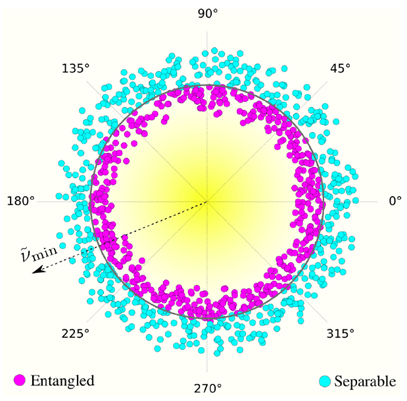
Simulation results showing how a Quantum Reservoir Processor recognizes entanglement in “squeezed-thermal” quantum states. The input states are characterized by two parameters: a “squeezing angle” that does not affect the degree of entanglement (plotted as the azimuthal angle), and a “minimum symplectic eigenvalue” governing the degree of entanglement (plotted as the radial distance, with smaller values corresponding to more entanglement). The magenta dots are the states identified by the Quantum Reservoir Processor as entangled, and the cyan dots are those identified as non-entangled. Figure excerpted from Ref. [1].
In a follow-up work published in IEEE Transactions on Neural Networks and Learning Systems in 2020, we showed that a Quantum Reservoir Processor is not limited to recognizing specific features of a quantum state, such as the degree of entanglement – it can perform a “tomographic reconstruction”, meaning that it can capture enough features of the quantum state to fully reconstruct it [2].
Simulation of quantum state tomography by a Quantum Reservoir Processor. The inputs to the Quantum Reservoir Processor are a set of quantum states described by two parameters, denoted by x (position) and p (momentum). The output of the Quantum Reservoir Processor, shown in the upper panels (a)–(c), accurately reproduces the parameters of the input states. The deviation between the state reconstruction and the actual input states is about one part in a thousand, as shown in the lower panels (d)–(f). Figure excerpted from Ref. [2].
Deeper Dives into the Quantum Reservoir
The Quantum Reservoir Processor that we have described thus far takes a quantum input (a quantum state to be analyzed) and produces a classical output (a set of numbers that characterize the state). In a paper published in Physical Review Letters in 2020, we showed that a Quantum Reservoir Processor can also be operated “backwards” – with a classical input and a quantum state as the output. In this mode of operation, the Quantum Reservoir Processor is able to generate quantum states with properties that are desirable for quantum information processing and other applications [3].
A natural follow-up question is whether quantum reservoir processors can operate with a quantum input and quantum output. This may be an interesting way to achieve a universal quantum computer.
In our formulation of Quantum Reservoir Processor concept, we have deliberately kept the theory general enough to be applicable to a wide variety of physical systems, many of which are already being developed for standard quantum computing applications. Previously, we have worked with experimental collaborators to develop classical reservoir processors based on lattices of nonlinear optical cavities [4], and such devices could be further developed into Quantum Reservoir Processor. Other possible experimental platforms include quantum dots in cavities, superconducting qubits in microwave resonators, and lattices of ultracold ions.
References