As previous projects had made use of COMSOL and Finite Element Analysis to come up with realistic targets and simulations of their setup, we sought out to do the same. Through various COMSOL models, we were able to obtain estimates of the velocity needed before the vehicle would overcome magnetic drag and levitate.
We started the COMSOL Model with 2D, followed by an upscale to 3D. This was to ensure that the 2D ‘foundation’ of the model was already efficient enough before moving onto the computationally heavy 3D modeling.
2D Modeling
The 2D COMSOL Modeling of our project was done using the Magnetic fields (mf), Moving mesh (ale) and Global ODEs and DAEs (ge) physics modules. Both stationary and time-dependent studies were conducted.
The 2D model served the main purpose of telling us what the minimum velocity the vehicle had to travel at before it would start levitating. Through inputting different minimum horizontal velocities, and outputting the graph of the net vertical force on the magnets, we would be able to tell if our velocity input caused levitation.
To ensure the efficiency of solving the model, we downscaled the model to an initial 4-magnet array (whereas multiple sets of 4 would be used in our actual setup), above a rectangular copper track.
A main challenge that we faced initially was the lack of knowledge / information on the parameters of our actual setup. To eliminate this problem, we tried to build / design prototypes concurrently, and used the parameters from those plans in the model.
Although the 2D model was supposed a simplification, we tried to keep our parameters as similar to the actual setup as possible to ensure higher accuracy in modeling.
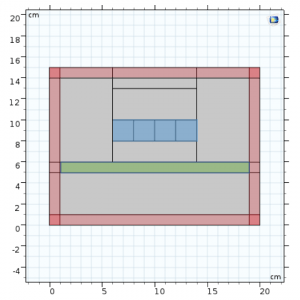
Parameters used in the 2D geometry:
- Mass of system = 80 g
- Horizontal velocity = varied to find minimum velocity needed for levitation
- Track thickness = 3 mm (material: copper)
- Magnet length = 1.5 cm
- Air gap = 4 mm
- Magnet remanent flux density = 1.38 T
In the image above, the pink regions account for the infinite element domains, to model a continuous environment with the surroundings. The region highlighted in green is the copper track; while that highlighted in blue are the 4 magnets.

By assigning different types and sizes of the mesh in our 2D model, we were able to increase computational efficiency and ensure that the model ‘zooms in’ to where the most interaction is occuring — the track and magnets. Mapped mesh was applied to the infinite element domains, with generally consistent rectangular shapes. On the other hand, free triangular meshing was applied to the remaining domains due to the versatility of this type of mesh.
By manipulating the model by using the necessary smoothing functions and global differential equations, we were able to study the various forces and velocity components involved in this setup.
The net vertical force on the magnet array was probed and measured in the model using respective necessary functions.


Solving the model produces the graph of the net vertical force on the magnets seen here. From these results, we know that the vehicle is oscillating in up and downward movements.
By varying the initial velocity input in this 2D model, we also found that the initial velocity needed for the vehicle to move is at least 10 m/s. This eventually tallied with the velocity needed in our actual prototype.
This video shows the animation of the levitation (in up and downward oscillating movement) of the magnets in the 2D COMSOL Model, with 10 m/s speed applied.
3D Modeling
It is worth noting that at this point, we had decided to use a circular track instead of a linear one (refer to Planning of Prototype for more) to keep our setup small-scale.
Moving on from the 2D model, we intended to create a 3D-replica of the setup, this time with the actual number of magnets — nine. The same 3 Physics modules (as in the 2D Model) were used.

However, after much consideration, we realised a model that is more similar to the actual set up is needed as the difference between angular and linear velocities is not negligible. Since we were no longer simply moving the vehicle linearly over a copper track, but spinning a circular track relative to it, we had to consider the circular motions as well. Linear velocity modeled in the 2D model would not be a good estimate for the angular velocity of our actual setup.

Parameters used in the 3D geometry:
- Mass of system = 80 g
- Angular velocity = varied to find minimum velocity needed for levitation
- Track height = 3 mm (material: copper)
- Track diameter (from centre of magnet to centre of ‘hole’ in track) = 15 cm
- Magnet length, breadth and height = 1.5 cm
- Air gap = 4 mm
- Magnet remanent flux density = 1.38 T
Hence, a new 3D Model with a cylindrical geometry was built using the Rotating machinery, magnetics (rmm) module.
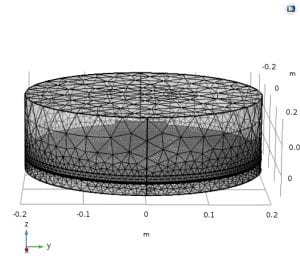
To increase the efficiency of the model, we also ensured an optimised meshing of the model. Since most of the ‘physics’ involved was around the track, we made sure to have a finer meshing of the track (especially because it was only 3 mm thick in the model).
From the 2D model, we managed to observe the up- and downward movement of the array over the track (illustrated by net vertical force on magnet).
In the 3D model, we decided to only calculate the upward Lorentz force on the array in order to increase solution efficiency. Once the upward Lorentz force is more than or equal to the weight of the array / vehicle, then that means that levitation will start to occur.

To first verify that our geometry and physics (e.g. direction of flux of each magnet according to the linear Halbach array arrangement) were correct, we conducted a stationary study with our model. Above is the flux density that we obtained in the solution. From the diagram, it is obvious that the main interaction (light blue areas) is between the magnets and the copper track. The yellow – red flux density of the magnets also tallies with what we expected to see. Together, these show that our model setup was correct.
Once this was verified, we proceeded to conduct a time-dependent study in which we attempted to find out the angular velocity (RPM) needed to exert an upward Lorentz force that is more than or equals to weight of the magnets — 80 g. Based on an estimate of 9.81 m/s² gravitational acceleration and mass of vehicle being 80 g, the weight of the vehicle would be 0.7848 N.
From our studies, for the upward Lorentz force to be more than or equals to 0.7848 N, the minimum angular velocity would be at least about 1400 RPM. With the diameter of the track of our actual setup being 15 cm, this would translate to about 39.6 km/h (11 m/s). This value is verified by the solution from our 2D model (which gave a minimum velocity of 10 m/s), as well as our actual setup (from which we obtained, experimentally, a minimum velocity of slightly above 11 m/s).

To further the study of the relationship between the angular velocity of the track and the upward Lorentz force exerted on the magnets, we also conducted a parametric sweep. Keeping duration / time constant, we varied the values of the angular velocity and measured Lorentz force (in z-direction) on the magnets for each velocity.
All in all, our COMSOL models have proven to be computationally efficient and more importantly, tallied with our experimental data. As part of our future work, we could aim to make our model more realistic and conduct more parametric studies to find out how different aspects of the setup affects the performance of the Hyperloop.
Credits
- https://www.comsol.com/blogs/meshing-your-geometry-various-element-types/
